前回
ed25519のpython実装を紐解く その1数学編 - Pebble Coding
はed25519のpython実装の数学編をやりましたが、今回は暗号編です。
暗号部分の関数を見ていきます。
これらの計算手順は前回と同じRFCに記載されています。
概念図を書いてみました。
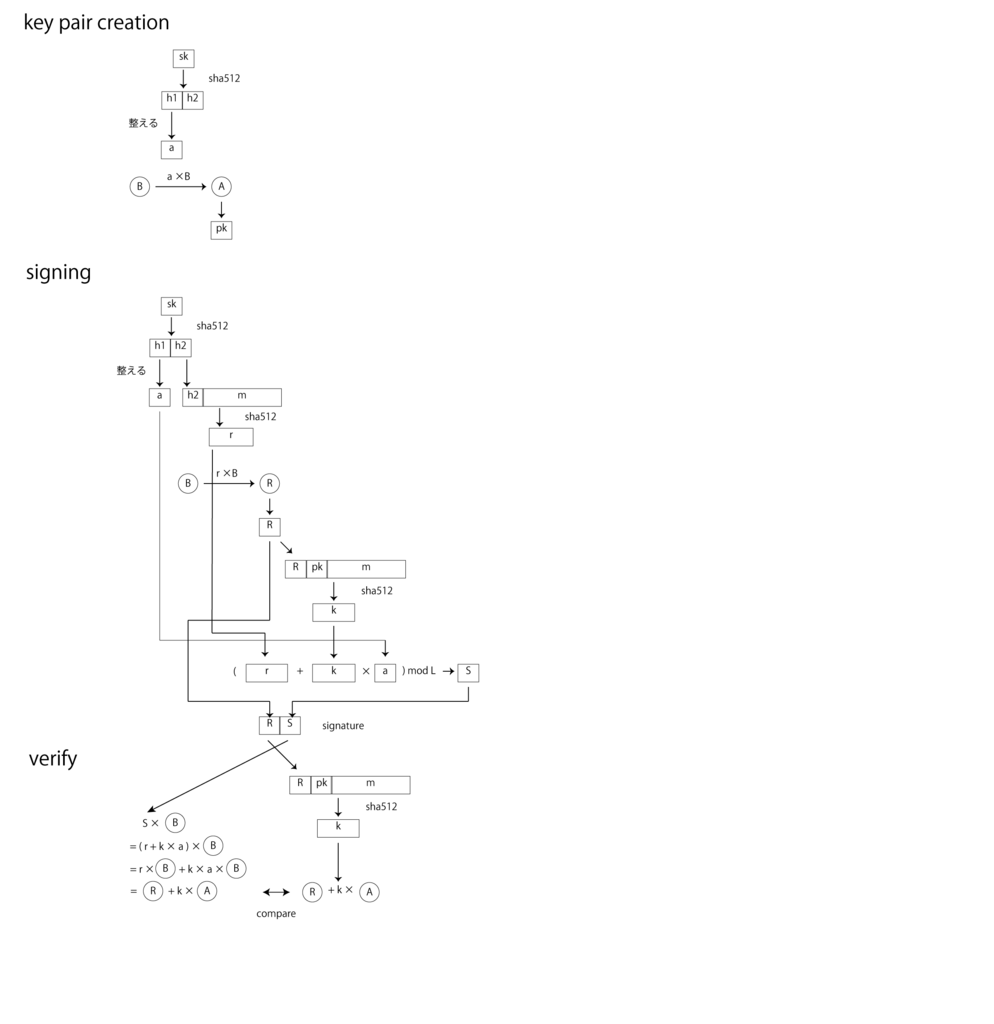
b = 256
秘密鍵の長さは256ビットつまり、32バイトのバイト列で表現できます。
公開鍵の長さも同じ32バイトのバイト列です。
秘密鍵は単純にランダムな32バイトのバイト列を生成すればそれで終わりです。(マジか)
公開鍵は秘密鍵から算出します。この手順は後で説明します。
def H(m): return hashlib.sha512(m).digest()
H()関数では、任意の長さのバイト列mのsha512を計算します。digest()関数は512ビットつまり、64バイトのバイト列を返します。
def bit(h,i): return (ord(h[i/8]) >> (i%8)) & 1
bit()関数ではバイト列hの上位(左側)から数えて(i/8)番目のバイトの、下位から数えて(i%8)ビット目が1か0かを返す関数です。
ordは1文字を整数のコードポイントに変換する関数です。
秘密鍵、公開鍵ペアの生成 (key pair creation)
def publickey(sk): h = H(sk) a = 2**(b-2) + sum(2**i * bit(h,i) for i in range(3,b-2)) A = scalarmult(B,a) return encodepoint(A)
publickey()関数は秘密鍵の32バイト列から公開鍵の32バイト列を返す関数です。
STEP1) 32バイト列の秘密鍵のsha512を計算し64バイト列を出力しhとします。
鍵生成にはhの上位32バイトのみを使います。
STEP2) 最上位バイトの最下位3ビットをクリアして8の倍数にします。
最下位(上位から32バイト目)の最上位ビットから2番目をセットします。
これは桁数を保証するためです。
最上位は0です。qより小さい値にするためです。
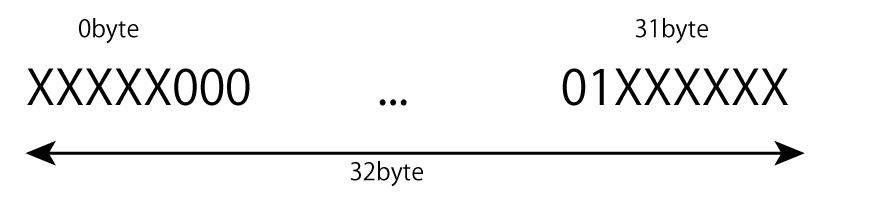
STEP3) 32バイト列をLittleEndianの正の整数(10進数で77桁)としてaとします。
以降LittleEndian整数化するときは常に正の整数とします。
ベースポイントBをスカラーa倍して点Aを計算します。
STEP4) 点Aの点座標を使ってある計算をします。
計算はencodepoint関数で実装します。
戻り値は32バイト列で公開鍵となります。
def encodepoint(P): x = P[0] y = P[1] bits = [(y >> i) & 1 for i in range(b - 1)] + [x & 1] return ''.join([chr(sum([bits[i * 8 + j] << j for j in range(8)])) for i in range(b/8)])
encodepoint(P)関数は点Pのx,y値を用いて、32バイト列を返します。
なので、点の座標は256ビット未満つまり32文字以内であることを理解しておきます。
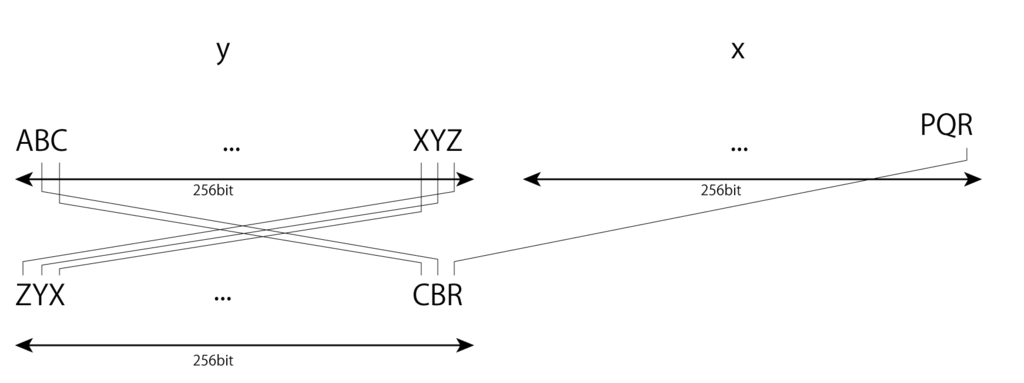
点Pのy座標値の整数をLittleEndianの32文字で表現します。
x,y座標は常に0以上、未満なので、256ビットの最上位ビットは常に0です。
そして256ビットのうちの最下位ビットをx座標値の最下位ビットの値に置き換えます。
こうしてできた0,1の256個の配列がbitsでそれを文字列に変換した32バイト列が戻り値です。
def encodeint(y): bits = [(y >> i) & 1 for i in range(b)] return ''.join([chr(sum([bits[i * 8 + j] << j for j in range(8)])) for i in range(b/8)])
関数encodeint(y)はy座標の整数値(256ビット)をLittleEndianとして32バイト列に変換します。
署名(signing)
def signature(m,sk,pk): h = H(sk) s = 2**(b-2) + sum(2**i * bit(h,i) for i in range(3,b-2)) r = Hint(''.join([h[i] for i in range(b/8,b/4)]) + m) R = encodepoint(scalarmult(B,r)) k = Hint(R + pk + m) S = (r + k * s) % l return R + encodeint(S)
signature()関数は、秘密鍵sk、公開鍵pkを使って任意の長さのバイト列mに署名(sign)した64バイト列を返します。
STEP1) 32バイトの秘密鍵のsha512を計算し64バイト列を出力します。これをhとします。
hの前半の半分の32バイトのバイト列に対して、最下位バイトの最下位3ビットをクリアします。
最後のバイト(下位から32バイト目)の最上位ビットをセットします。これをsとします。
STEP2) hの後半の32バイトに任意の長さのバイト列mを加え、sha512を計算して出力した64バイト列をLittleEndianで整数(512bitなので10進数で約155桁)にして、これをrとします。
STEP3) ベースポイントBをrスカラー倍した点のencodepointを計算し、32バイト列を作りRとします。rは10進数で約155桁ほどです。
STEP4) 32バイト列のR、32バイト列の公開鍵、任意のバイト列のmを結合して、sha512を取り、LittleEndianとして64bitの整数にしてkとします。
STEP5) S = (r + k * s) mod Lを計算します。
STEP6) 32バイトのRとSのLittleEndian化した32バイトを結合した64バイト列を署名とします。
def Hint(m): h = H(m) return sum(2**i * bit(h,i) for i in range(2*b))
Hint()関数は任意長のバイト列のsha512を取って512ビット(=64バイト)のバイト列をLittleEndianとしての整数を返します。
Verification(署名確認)
def checkvalid(s,m,pk): if len(s) != b/4: raise Exception("signature length is wrong") if len(pk) != b/8: raise Exception("public-key length is wrong") R = decodepoint(s[0:b/8]) A = decodepoint(pk) S = decodeint(s[b/8:b/4]) k = Hint(encodepoint(R) + pk + m) if scalarmult(B,S) != edwards(R,scalarmult(A,k)): raise Exception("signature does not pass verification")
64バイト列の署名s、任意長のメッセージm、32バイト列の公開鍵pkを用いて、このメッセージを署名確認し、
確認できない場合は例外を送出します。
STEP1) 署名の前半32バイト列を点Rにデコードします。
公開鍵を点Aにデコードします。
署名の後半32バイト列をLittleEndianで正の整数Sにデコードします。(Sは0以上L未満です。)
STEP2) 点Rをエンコードした32バイト列、32バイト列の公開鍵、任意長のメッセージバイト列を結合し、512ビットの整数kとします。
STEP3) ベースポイントBをSスカラー倍した点と、点Rに、点Aをkスカラー倍した点を加算した点が等しいかどうかを確かめます。
def decodeint(s): return sum(2**i * bit(s,i) for i in range(0,b))
decodeint()関数は、encodeint()の逆関数で、32バイト列をLittleEndian整数に変換します。
def decodepoint(s): y = sum(2**i * bit(s,i) for i in range(0,b-1)) x = xrecover(y) if x & 1 != bit(s,b-1): x = q-x P = [x,y] if not isoncurve(P): raise Exception("decoding point that is not on curve") return P
decodepoint()関数はencodepoint()関数の逆関数で、
32バイト列sからy座標の値に変換します。256ビットの最上位ビットは常に0なので、無視します。
このy座標の値からx座標の値を求めます。x座標の値の偶奇が一致しない場合は、一致したxの値に置き換えます。
これが点Pの座標となるので関数の戻り値としますが、ここでは攻撃を防ぐためさらに、楕円関数上の点であることを確認しています。
秘密鍵を使ってベースポイントをaスカラー倍した点Aの座標は公開するけれども、
どのくらいスカラー倍したかは公開しないとしていることが分かります。
また、ベースポイントをLスカラー倍すると無限遠点になることを用いていることも分かります。
なお、下位3ビットをクリアして8の倍数にしている理由はこちらを参照ください。
この曲線のcofactorが8であることと関係があります。